La notion de forces en physique est très importante, vous direz
peut être que ça l'est moins que l'énergie
qui est indispensable à la vie, mais sans force, il n'y aurait
pas d'énergie transférée.
Vous savez tous ce qu'est une force, quiconque est capable de me citer
un exemple.
En voici quelques-uns
Deux personnes qui font un bras de fer.
Une paire de boeufs tirant une charrue.
Un moteur en train de réaliser une tâche comme
entraîner une scie coupant du bois
Une fillette qui tire de l'eau au puits
Etc. etc. etc.
Ces exemples ne suffisent pas au physicien, ils font tous allusion
à un contact, mais comme nous allons le voir plus loin, une
entité ne nécessite pas obligatoirement de toucher un
objet pour
lui soumettre une force.
Vous savez déjà que les objets tombent à terre
quand on
les lâche et qu'un aimant attire les clous, sans qu'il y ait
pourtant
de contact.
Par contre les premiers exemples suffisent à définir une
force comme quelque chose capable d'effectuer un travail ou
énergie mécanique.
La force peut être définie de la façon suivante :
W = Fxd
W = énergie en Joule
F = force en Newton
d = déplacement dans le même sens que la force, en
mètre.
Voir "énergie"
La force est alors définie comme suit :
Une force de 1 Newton est la force qui développe une
énergie de 1 Joule quand on l'applique en se
déplaçant de 1 mètre.
Mais on peut aussi définir l'énergie par :
Une énergie de 1 Joule est l'énergie produite par une
force de 1 Newton se déplaçant de 1 mètre.
On tourne en rond!
On décide de garder la définition pour l'énergie,
et de trouver autre chose pour la force, nous verrons plus loin ce
qu'il faut adopter.
Dans l'exposé sur l'énergie, on a vu qu'une force pouvait
s'opposer à un poids.
Mais comment s'opposer à un poids de 50 kg, puisqu'une force
s'exprime en Newton?
Tout simplement parce qu'un poids de 50 kg n'existe pas, pas plus que
de toute autre quantité de kg, il s'agit là d'une erreur
de langage.
Quand on dit qu'un objet fait 50 kg, il ne s'agit pas de son poids mais
de sa masse, une masse de 50 kg correspond à un poids d'environ
500 N
Mais alors qu'est ce qu'une masse ?
Qu'est ce qu'un poids ?
La masse est une quantité de matière.
Mais alors plus l'objet est volumineux, et plus sa masse est importante
?
La réponse est oui, si l'on compare deux objets, le plus gros
sera le plus massif, à condition qu'ils soient de même
matériau.
Une bouteille pleine de trois litres d'eau sera plus massive qu'une
bouteille contenant un seul litre du même liquide, pourtant un
récipient contenant un litre de mercure sera plus massif
qu'un récipient contenant 10 litres d'eau.
Mais alors comment comparer la masse de deux objets de matériaux
différents?
Il faut considérer l'aspect atomique.
Tous les objets qui nous entourent sont constitués de
molécules comprenant des atomes qui eux mêmes comprennent
des protons et des
neutrons.
Il peut y avoir plusieurs molécules si l'objet est un
mélange.
Les molécules sont des ensembles de plusieurs atomes.
Les atomes comprennent un noyau autour duquel gravitent des
électrons, les noyaux sont composés de protons et de
neutrons.
Protons neutrons et électrons sont considérés
comme des billes mais cette image n'est qu'un modèle, les atomes
ont un rayon de l'ordre de grandeur l'Angström soit 10^-10
m,
ils ne sont pas visibles.
Les protons et les neutrons sont tous identiques, le proton d'un atome
de mercure est le même que celui que l'on peut trouver dans une
plume d'édredon.
Il suffit de compter les protons et les neutrons dans un objet pour
connaître la masse, même si cette affirmation n'est pas
rigoureusement exacte, elle est très proche de la
réalité, en tout cas elle a le mérite de montrer
ce qu'est la masse.
Exemple :
Un atome de carbone possède 6 protons et 6 neutrons, sa masse
est donc de 12
Quelle unité donner à la masse?
Un atome est quelque chose de très petit, l'unité de
masse du nucléon (les protons et les neutrons sont nommés
nucléons car ils constituent le noyau de l'atome) est
l'unité de masse atomique (uma).
Par définition, un nucléon a une masse de 1 uma
Les puristes vont dire que le neutron et le proton ne font pas la
même masse, qu'il faut aussi compter la masse des
électrons, les isotopes etc, c'est vrai mais il faut penser que
ce document s'adresse à des personnes qui découvrent ces
premières notions de physique, il convient d'apporter les choses
au fur et à mesure, nous y viendrons.
L'atome de carbone a une masse de 12 uma
L'atome d'hydrogène a un seul nucléon qui est un proton,
sa masse est donc 1 uma
Nombre d'Avogadro
L'atome est une entité trop petite pour notre vie de tous les
jours, nous préférons utiliser la mole qui
représente une quantité très grande.
1 mole = 6,02x10^23
1 mole d'atomes contient 6,02x10^23 atomes
1 mole d'atomes d'hydrogène a une masse de 1 gramme, on peut
donc définir provisoirement le gramme comme la masse de 1 mole
de nucléons.
Mais comme on s'en doute, on ne pourra pas mesurer la masse d'un objet
en comptant ses nucléons, ils sont bien trop nombreux, il faudra
faire une mesure indirecte
comme nous le verrons.
D'ailleurs dans les usines, le comptage de petits objets se fait par
une pesée.
Une mesure indirecte consiste à déterminer une grandeur
en en mesurant une autre, par exemple on peut mesurer la longueur d'un
fil électrique avec un mètre , dans ce cas, on effectue
une
mesure directe, mais si on fait la mesure avec un
ohmmètre, cette fois on fait une
mesure indirecte en utilisant la propriété de
proportionnalité entre la résistance électrique et
la longueur.
On retiendra, puisque la masse est définie comme le nombre de
nucléons, que cette grandeur ne dépend que de l'objet et
non de sa position.
Une masse de 1
kg fera toujours 1 kg qu'elle soit sur terre, sur la lune ou dans
l'espace.
L'unité légale de masse est le kilogramme.
On définit le kilogramme comme étant la masse d'un
prototype en platine iridié conservé
précieusement sous cloche dans un musée.
Bien entendu cet objet est unique car il représente
l'étalon de référence, cependant d'autres
étalons sont utilisés pour étalonner des balances,
mais ceux-ci sont moins précis déjà parce que par
définition c'est le premier qui est pris comme
référence et aussi parce que davantage manipulés,
ils s'usent plus vite.
L'étalon de référence n'a été sorti
que trois fois depuis sa création, et cela a suffit pour qu'il
perde quelques microgrammes!
On définit le poids d'un objet comme étant la force avec
laquelle il est attiré vers le sol.
Contrairement à la masse, le poids dépend du sol (sol
lunaire, sol terrestre, plancher du vaisseau spatial...)
En effet, vous avez entendu dire que sur la lune, les astronautes
pouvaient sauter comme des cabris.
Le poids est proportionnel à la masse, quand vous soulevez un
objet, vous opposez une force au poids, s'il y a deux objets
identiques à soulever, l'effort à déployer sera le
double.
g est une constante de proportionnalité dépendant du
lieu, dans le cours sur l'énergie, il a été
démontré que le poids soumettait l'objet à une
accélération dont la valeur n'est autre que g.
Donc
F = force en Newton
m = masse en kilogrammes
g = accélération en mètres par seconde chaque
seconde que l'on note (m/s)/s ou encore m.s-2
La valeur de g dépend du corps céleste, chaque
planète
possède une valeur de g, celle de la terre est 9,81.
Exercice d'application :
Quel est le poids sur terre d'une masse de 15 kg ?
Réponse :
Le poids étant donné par le produit m.g, avec g sur
terre = 9,81 on
obtient :
F = mg = 15x9,81 = 147,15 N
Ne soyons pas choqués d'exprimer un poids en Newton et de le
noter F, car le poids est une force.
Certains préfèrent utiliser le kilogramme pour
unité de poids, vous avez raison d'utiliser le kilogramme pour
les produits
alimentaires que vous achetez car c'est d'une masse dont il
s'agit, je l'ai déjà dit mais je n'insisterai jamais
assez.
Une masse est une quantité de matière et s'exprime en
kilogrammes
Un poids est une force exercée par un corps céleste*, sur
un
objet.
*Cette définition de la force est incomplète, il n'y a
pas
que des corps célestes, telles la terre ou la lune qui puisse
attirer les objets, deux objets de petite taille exercent aussi une
force d'attraction mais elle est si faible qu'il est difficile de la
mettre en évidence.
Il existe d'autres types de forces davantage visibles comme celle des
aimants avec le fer.
Maintenant que l'on a compris ce qu'est une masse et un poids, comment
faire pour les mesurer ?
Un poids est une force, il existe un appareil capable de mesurer
une force, il s'agit d'un dynamomètre.
Un dynamomètre est un ressort avec un index qui se
déplace le long d'une règle graduée.
On sait que deux objets de même matériau et de même
volume ont la même masse car ils ont le même nombre de
nucléons.
La masse réunissant ces deux objets sera 2m, si celle d'un objet
est m.
Le poids de cet ensemble sera 2mg soit deux fois le poids d'un seul
objet, on constate un étirement du ressort qui est le double par
rapport à ce qu'il serait si on accrochait un seul objet au bout.
On a donc dF = kdx
dF = petite force exercée sur le ressort
dx = petit allongement
k = constante de raideur qui est un paramètre du ressort,
dépendant du matériau et de la grosseur de ses spires.
Si la force et l'allongement ne sont pas petits, la relation reste
valable, tant que l'on n'a pas atteint la limite
d'élasticité du ressort.
On sait donc mesurer un poids, il suffit de mesurer la longueur d'un
ressort et connaissant la constante k, graduer une échelle.
Exercice de
compréhension.
Une fois que la graduation est faite, le dynamomètre aura t-il
besoin d'une graduation différente si on mesure un poids sur la
lune ?
Justifiez votre réponse.
La correction sera donnée plus loin.
Si on se reporte à la définition, une masse correspond
à un nombre de nucléons, il est impossible de les compter
vu leur nombre, mais nous pouvons déterminer la masse d'un objet
d'après son poids car :
F = mg
Nous connaissons g, sur terre il vaut 9,81
F est donné par un dynamomètre, il ne reste plus
qu'à trouver m.
Mesure indirecte.
Nous avons fait une mesure indirecte, car nous déterminons la
masse en mesurant le poids.
Exemple :
Le poids d'un objet a été mesuré sur terre, avec
un dynamomètre, sa valeur est 9,81 N quel est sa masse ?
m = F/g = 1 kg
Inconvénient de cette méthode.
La valeur g donnée ne fait pas 9,81 sur toute la surface du
globe, comme on le verra par la suite, ce qui fait que toute balance
fonctionnant sur le principe de déformation élastique
d'une jauge, doit être étalonnée là
où elle se trouve.
Une balance est un instrument qui donne une masse, elle peut être
construite avec un ressort comme un dynamomètre mais
graduée en kilogramme et doit être étalonnée
là ou elle est utilisée.
Une balance de ce type étalonnée à Lyon ne pourra
pas être utilisée à Paris sans qu'il soit fait un
nouvel étalonnage, en tout cas si on veut être rigoureux.
Réponse à
l'exercice de compréhension.
Un dynamomètre est fait pour mesurer une force ou un poids, vous
pouvez l'utiliser pour une masse, il suffit de graduer la
réglette en
kg en suspendant des masses connues, mais dans ce cas vous ne pourrez
pas utiliser
l'appareil ailleurs que là où il a été
étalonné.
Un dynamomètre gradué sur terre n'a pas besoin d'une
graduation différente sur la lune si celui-ci a
été conçu pour sa vraie utilisation, la mesure de
forces.
Le poids d'un objet sur la lune est environ six fois plus faible que
sur terre, l'allongement du ressort sera six fois plus faible donc
l'index va bien indiquer un poids six fois plus petit.
Par contre une balance de type dynamométrique utilisée
sur terre serait archi fausse
sur la lune.
Mesure plus directe.
Quand je dis mesure directe, il ne s'agit pas de compter les
nucléons mais de comparer la masse inconnue d'un objet à
des masses connues marquées.
Cet appareil est une balance à plateaux, voici le principe.
On place l'objet à mesurer sur un plateau et des masses
marquées sur l'autre.
Quand l'équilibre est réalisé, la masse de l'objet
est égale à celle des masses marquées.
Sur la lune, une balance de ce type fonctionne encore, certes le poids
de l'objet est plus faible mais celui des masses marquées est
aussi plus faible dans les mêmes proportions, l'équilibre
se conserve.
Cette méthode n'est pas directe à 100% car il faut quand
même qu'il y ait un poids qui s'exerce sur les
éléments à comparer, une balance de ce type ne
fonctionnerait pas dans l'espace.
Nous donnerons des méthodes pour mesurer une masse dans l'espace.
Pourquoi deux masses identiques équilibrent-elles les plateaux
d'une balance? existe t-il une condition particulière?
Imaginons une planche sur un pivot non centré et une masse
à chaque bout.
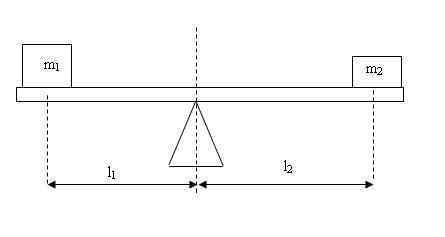
Quel est la masse qui va être en bas et celle qui va être
en haut ?
C'est la loi de l'énergie potentielle minimale qui va permettre
de répondre à la question.
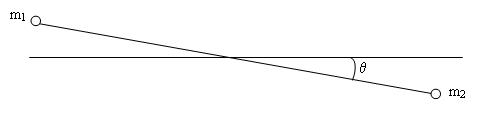
L'énergie potentielle des deux masses réunies est
donnée par :
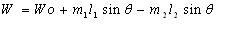
Wo étant l'énergie potentielle de l'ensemble des deux
masses quand le système est en équilibre.
Il n'y a pas besoin de dériver et de dire que la
dérivée est nulle car cette fonction n'a pas d'extremum.
W sera d'autant plus petit m1.l1
sera petit et que m2l2 sera
grand, ce
qui veut dire que la balance penche du côté où le
produit ml est le plus grand et non vers celui où simplement m
est le plus grand.
Cette affirmation signifie qu'une balance ne peut comparer des masses
que si la longueur des bras est identiques, cela va jusqu'à dire
que les masses doivent être placées au centre des plateaux.
Un trébuchet est une balance dont les plateaux sont suspendus,
la
précision de la mesure est meilleure car le centre de
gravité des masses est à égale distance par
rapport au pivot.
On peut mettre le terme sinus en facteur.

Pour que l'énergie soit minimale il faut non seulement que
m1.l1<m2l2 mais il faut aussi que l'angle
d'inclinaison soit la plus grand possible, ce
qui signifie qu'une balance penche au maximum lorsque les masses sont
différentes.
L'angle maximal est 90° dont le sinus vaut 1, ce qui veut dire que
si le pivot est assez haut pour que les plateaux ne puissent pas
toucher par terre, les bras vont se mettre à la verticale, vous
vous en doutiez sûrement mais encore fallait-il dire pourquoi.
Arrivé jusqu'ici, vous devez savoir faire la différence
entre une masse et un poids et savoir comment on peut mesurer l'un et
l'autre, pour le poids il faut un dynamomètre et pour la masse,
une balance suffit pratiquement partout sauf dans l'espace en l'absence
d'attraction.
On verra plus loin comment mesurer une masse dans l'espace.
Le poids est une force, on a démontré dans le cours sur
l'énergie, que le poids soumettait un objet à une
certaine accélération telle que v = gt
La vitesse croît linéairement par rapport au temps.
g est l'accélération de la pesanteur.
On a vu aussi que le poids F = mg
La masse m est nommée masse pesante, car elle fait intervenir le
facteur g traduisant le poids.
Nous pouvons, à partir de cette affirmation
généraliser la relation pour toutes les forces, que
celle-ci soit due à la pesanteur exercée par un corps
céleste ou qu'au contraire elle soit produite par un animal.
Dans tous les cas F = ma
F est la force exercée sur un objet de masse m.
Cette masse est nommée masse inerte, car elle se traduit par la
difficulté qu'il y a pour la mettre en mouvement.
Le choix judicieux pour g, a fait que la masse inerte et la masse
pesante sont identiques, on appellera tout simplement masse le terme m.
Sous l'action de cette force, la vitesse de l'objet va augmenter, telle
que dv/dt = a
a est l'accélération, qui est égale à g si
la force est un poids.
Cette relation vous semble probablement fausse, car lorsque vous
poussez une voiture pour la faire démarrer, vous constatez que
sa vitesse n'augmente pas toujours, et si vous essayez de tirer la tour
Eiffel elle ne bougera pas du tout.
Le problème en physique c'est que l'attraction terrestre masque
beaucoup de choses et pour analyser une loi, il faut prendre un
système isolé qui est l'espace.
Dans l'espace, vous pourriez déplacer une masse aussi importante
que la tour Eiffel, bien difficilement car vous flotteriez et vous ne
pourriez pas communiquer beaucoup de force, mais sachez que ce serait
possible.
Prenons un autre exemple.
Si vous êtes dans l'espace et que vous communiquez une force de
10 N à une balle de 1 kg, la vitesse de la balle va augmenter.
Si au départ la balle est immobile, au bout de 1 seconde sa
vitesse sera de 10 m/s au bout de 2 s elle vaudra 20 m/s au bout de 3 s
ce sera 30 m/s et ainsi de suite jusqu'à ce que vous la
lâchiez.
Il est important que pendant que la balle est tenue vous lui
communiquiez un effort constant, sinon il faut analyser chaque
intervalle de temps et écrire l'équation
différentielle.
F = mdv/dt
On intègre 1/mF(t)dt pour connaître v.

Maintenant placiez vous sur terre et exercez votre force vers le haut.
La balle ne bouge pratiquement plus car votre force est
contrebalancée par le poids.
Soit 10 N pour la force et 9,81 N pour le poids.
La balle va donc monter avec une vitesse qui va croître de 0,19
m/s ce qui n'a rien à voir avec la cas de tout à l'heure.
En ce qui concerne la tour Eiffel, vous pourriez
l'accélérer si
elle était posée et non fixée, et il faudrait que
la composante longitudinale du poids soit nulle c'est à dire que
le sol soit parfaitement de niveau.
Enfin le sol devrait être parfaitement lisse pour ne
présenter aucune force de frottement.
Sa masse est de 10100 tonnes, si vous exercez une force de 1000 N,
l'accélération sera de : 0,000091 m/s soit 91 microns par
seconde par seconde.
Un dénivelé de un millimètre pour 100
mètres et vous subissez le cent millième du poids
de la tour Eiffel, c'est à dire 101 kg.
Vous êtes en droit d'affirmer que tout ceci est absurde que la
tour Eiffel on ne peut pas la bouger car de toute façon il n'est
pas possible sur le plan matériel de prouver le contraire.
En physique nous observons des phénomènes grâce
à
des mesures qui sont possibles, et de là nous établissons
des lois en pensant qu'elles vont fonctionner dans tous les cas,
même ceux pour lesquels la vérification
expérimentale est impossible.
Mais si on veut avancer on est obligé de faire ainsi, et le jour
où on constate quelque chose de nouveau, la loi s'écroule.
Nous appliquerons donc la loi F = ma dans le cas où les forces
mises en jeu sont connues et si certaines sont inconnues, il faudra
qu'elles soient suffisamment petites pour pouvoir les négliger.
Dans les problèmes de physique, nous travaillons avec des
variables qui sont du même ordre de grandeur, parce que
généralement l'environnement fait que l'on doit tenir
compte d'autre phénomènes comme les forces de frottement,
la résistance de l'air etc.
Si F représente des Newton, alors m représente des
kilogrammes et non des pico grammes et inversement, sauf si on
travaille
dans l'espace loin de toute autre influence.
PREMIERE LOI DE NEWTON
Principes
Revenons dans l'espace, et considérons un espace galiléen.
Un espace est dit galiléen s'il ne subit aucune
accélération, on le dote d'une origine et de trois axes x
y z
Un objet immobile reste immobile.
Un objet en mouvement avec une vitesse constante, conserve sa vitesse
si aucune force ne s'applique dessus.
Ceci est la conséquence de F = ma, si F = 0 alors a = dv/dt = 0
Une force peut accélérer un objet, le ralentir ou changer
sa
direction.
En effet changer de direction, c'est changer la composante d'une
vitesse.
Nous allons, à ce sujet présenter la force centrifuge,
mais avant, déterminer comment on peut mesurer une masse dans
l'espace.
Puisqu'il n'y a pas de pesanteur, il n'y a pas de poids, donc une
balance classique ne fonctionne pas.
Vous pouvez tirer sur un objet pour l'accélérer,
mais si vous ne connaissez pas votre
force, vous pouvez la mesurer en insérant un
dynamomètre entre l'objet et vous
et vous passez devant une série de faisceaux lumineux
captés par une cellule photoélectrique, dont vous
observez le signal sur un oscilloscope, afin de connaître
l'accélération.
Si vous êtes sûrs qu'il existe trois cellules successives
devant lesquelles le ressort du dynamomètre
s'est étiré toujours de la même longueur, vous
pouvez observer les durées entre ces coupures de faisceaux;
L'espace entre les cellules étant connu et égal à
dx, la vitesse entre les deux premières cellules vaut :
v1 = dx/(t1-to)
Et la vitesse entre la deuxième cellule et la
troisième vaut :
v2 = dx/(t2-t1)
Au temps t1 on connaît la vitesse v1 et au temps t2, on
connaît
la vitesse v2, on en déduit l'accélération :
a = (v2-v1)/(t2-t1)
La mesure n'est pas simple, il faut veiller à ce que le ressort
(dynamomètre) soit toujours étiré de la même
longueur, on pourrait augmenter la distance entre les cellules 2 et 3,
ce qui obligerait à courir de plus en plus vite en essayant de
garder une accélération constante.
Enfin, comme on l'a dit, si le nombre de cellules est important,
on en observera bien 3 consécutives telles que le
dynamomètre indique la même force.
Maintenant, parlons de la force centrifuge.
On peut engendrer une force sans qu'il n'y ait
d'accélération, ou plutôt sans augmenter le module
de la vitesse, mais en changeant sa direction.
La force centrifuge fait l'objet
d'un document séparé.
Exercice.
Voici un exemple typique dans lequel la force centrifuge rentre en
compte.
On se propose de relever un virage pour éviter que les
véhicules dérapent.
Sachant que le rayon du virage est de 10 mètres et que les
véhiculent roulent à 50 km/h calculer :
Le poids d'un camion de 10 tonnes
La force centrifuge exercée sur le camion.
L'angle dont il faut relever le virage pour que l'adhérence soit
optimale.
Mêmes questions pour une voiture de 500 kg roulant à la
même vitesse.
Pour l'accélération on peut prendre 10, ce qui n'est pas
très éloigné de 9,81.
Si vous ne savez pas calculer l'angle, vous pouvez attendre d'avoir
parcouru le chapitre "représentation d'une force"
La réponse sera fournie un peu plus loin.
En attendant que peut-on dire de la force centrifuge?
Puisque cette force est engendrée par un mobile en rotation, il
est plus simple de mesurer la masse d'un objet en le faisant tourner
plutôt qu'en l'accélérant sur un parcours
rectiligne.
En effet en faisant tourner un objet fixé au bout d'un
dynamomètre, on mesure facilement le rayon, la vitesse et la
force, il ne reste plus qu'à déterminer la masse.
Ce système fonctionne sur la terre, sur la lune et dans
l'espace, en l'absence de toute pesanteur, nous ferons des exercices
d'application après avoir appris à
représenter une
force et à en additionner plusieurs.
Nous pouvons déjà répondre aux premières
questions
de l'exercice.
Le poids d'un camion de 10 tonnes fait :
10 000 x 10 = 100 000 N (on a pris 10 au lieu de 9,81 pour simplifier).
Force centrifuge:
F = mv²/R
v = 50 km/h = 50 000 m/h = 50 000/3600 m/s
v = 13,9 m/s
F = 10 000x13,9²/10 = 192 900 N
En ce qui concerne la voiture de 500 kg
Poids
F = 500x10 = 5000 N
Force centrifuge
F = 500x13,9²/10 = 9660,5 N
La fin de cet exercice sera corrigée plus loin.
Un objet en mouvement peut être entraîné par une
force décomposable en deux, une tangentielle et une centrifuge.
F = maT + maR
aT = d²v/dt² qui est l'augmentation de la vitesse de
l'objet sur sa trajectoire, par rapport au temps.
maR = mv²/R force centrifuge.

Voir démonstration "rayon de courbure"
| REPRESENTATION
D'UNE FORCE |
Jusqu'à maintenant nous avons considéré des
forces comme des quantités scalaires, c'est à dire ayant
une valeur avec un signe positif ou négatif et deux directions
possibles, le poids (vers le bas), la force que l'on oppose au poids
(vers le haut), la force centripète (vers le centre d'un virage)
la force centrifuge (vers l'extérieur d'un virage).
Mais on se doute que des forces ne font pas que s'additionner ou se
soustraire, si deux personnes tirent une charge avec chacune un effort
de 500 N, la somme des forces ne sera pas forcément 0 ou 1000 N,
cela
dépendra du sens de déplacement des personnes.
Ces considérations font que les forces sont de nature
vectorielle.
Mais le vecteur est généralement défini comme une
classe d'équivalence.
Deux représentants de cette classe correspondent à un
même vecteur.
Il est vrai que deux personnes tirant un objet à l'aide d'une
corde vont conjuguer leurs effort indépendamment de l'endroit
où ces personnes vont être placées;
Pourtant si on exerce les deux forces du même côté
d'une balançoire ou de chaque côté, le
résultat n'est pas le même.
Par conséquent, il vaut mieux définir une force avec son
point d'application, c'est à dire non pas seulement comme un
vecteur en tant que classe d'équivalence mais comme un vecteur
en tant que représentant de cette classe.
Un vecteur se représente avec un trait dont une
extrémité est le point d'application, on place la
flèche à l'autre extrémité.
La longueur du trait représente l'intensité ou module de
la force, la flèche indique le sens.
Somme de deux forces :
la somme de deux forces est simples, puisqu'une force est
représentée par un vecteur, il suffit de faire une somme
vectorielle.
Pour additionner deux vecteurs, on amène l'origine du
deuxième à l'extrémité du premier, la somme
est le vecteur qui part de l'origine du premier et qui
s'arrête à l'extrémité du deuxième.
La somme vectorielle est commutative
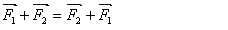
Décomposition d'une
force.
Toute force peut se décomposer en une somme de plusieurs forces,
deux forces ou trois forces et même davantage, il n'y a aucune
limite.
La décomposition peut se faire d'après un repère
orthonormé.
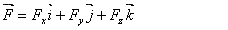
La décomposition peut se faire aussi par rapport à une
trajectoire, voici deux cas:
Le premier : Un mobile se
déplace sur une trajectoire
curviligne, (nous en avons déjà parlé).
Nous pouvons observer deux types d'accélération sur cette
ligne, une accélération tangentielle,
caractérisée par une vitesse de déplacement sur
cette ligne qui croît, et une accélération
centrifuge due au fait que la trajectoire se courbe.
Dans un déplacement, zéro force , une seule force
ou les deux forces peuvent être présentes
Une trajectoire rectiligne uniforme signifie : pas de force
Si la trajectoire est une droite et que le mouvement est
accélérée, alors la force est tangentielle.
Si la trajectoire est curviligne, et que la vitesse sur la courbe est
constante,
la force est centrifuge (ou centripète selon celle que l'on
considère).
Si la trajectoire est curviligne, et que la vitesse sur la courbe
est accélérée, il y a une composante centrifuge et
une
composante tangentielle.
Le deuxième, masse
posée sur un plan incliné.
L'objet est soumis à son poids.
Il est commode de décomposer le poids en deux forces dont l'une
est dans le sens de la planche et l'autre lui est orthogonale.
La composante parallèle à la planche indique que l'objet
va glisser dessus, et nous donne la valeur de la force qu'il faudra
communiquer à l'objet pour l'empêcher de bouger.
La composante orthogonale à la planche nous donne une indication
sur l'effort que fournit la planche face au poids de l'objet.
Exemple :
On pose un objet de masse 40 kg sur une planche inclinée de
10°
La planche plie de 0,1 mm par Newton appliqué
perpendiculairement à elle.
Quel effort faut-il fournir pour l'empêcher de glisser.
De combien se plie la planche?
Réponse à la dernière partie de l'exercice de la
force centrifuge.
Si on veut que le camion ou la voiture soit stable, il faut que la
force résultante soit orthogonale à la route.
Pour le camion :
Poids = 100 000 N
Force centrifuge = 192900 N
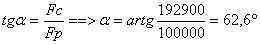
Pour la voiture :
Poids = 5000 N
Force centrifuge = 9645 N
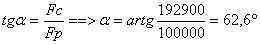
On trouve pareil que pour le camion, ce qui est normal, car si on
exprime de façon littéraire :
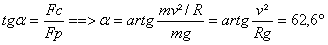
En réalité, on ne relève pas autant les virages,
car il faut aussi pouvoir rouler moins vite sans glisser, si on fait le
calcul pour 40 km/h voici ce qu'on obtient :

Pour 30 km/h
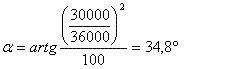
Pour 20 km/h
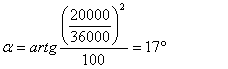
Il est clair que le fait de relever un virage ne sera efficace à
100% que pour une vitesse, mais pour les autres cela apportera
toujours quelque chose . Le fait de le relever à 17°
diminuera l'effet de dérapage pour tous les véhicules
roulant à plus de 20 km/h, par contre cela va amener les
véhicules roulant en dessous à glisser;
On parle de dérapage quand un véhicule tend à
aller vers l'extérieur du virage et de glissement lorsqu'il tend
à aller à l'intérieur.
Dans les deux cas se sont les forces de frottement des pneus ou
adhérence, qui s'opposent à ce que le véhicule
quitte la route.
Réponse à l'exercice précédent.
Un objet a une masse de 40 kg son poids est donc de 400 N
La planche est inclinée de 10°
La composante tangentielle à la planche vaut :
Ft = 400xsin10 = 69,45 N, c'est l'effort qu'il faut fournir pour
l'empêcher de glisser.
La composante orthogonale à la planche vaut :
Fo = 400xcos10 = 393,9 N, c'est l'effort que subit la planche,
puisqu'elle plie de 0,1 mm/N elle va donc s'incurver de 39,39 mm
Nous énonçons une règle : les forces sont toujours
en équilibre, ce qui veut dire :
Il y a autant de forces qui tirent que de forces qui poussent, ou plus
exactement la somme vectorielle des forces qui tirent est égale
à la somme vectorielle des forces qui poussent.
S (Fi) = S (Fj)
Cette définition est la même que la
précédente, on donne simplement le signe moins à
l'un des types par exemple celles qui poussent.
Mais avec les vecteurs, les forces peuvent être dans des
direction quelconque, et pas seulement dans deux directions distinctes,
et on a aussi :
S(Fi) = 0
Vous n'êtes pas obligés de me croire, mais je n'invente
rien, cette loi je l'ai apprise, un système de forces est
toujours en équilibre, je vais tenter de justifier cette
affirmation.
Commençons par l'équilibre statique.
Forces en équilibre statique.
Un ensemble de forces est en équilibre statique si le
système est immobile.
Ce genre d'équilibre est simple à expliquer.
Vous portez un seau d'eau, vous exercez une force égale au
poids, pas moins car le seau ne tombe pas et pas plus car il ne monte
pas plus haut que la position de votre main.
La force que vous exercez équilibre le poids, ces deux forces
sont identiques.
Si on trace un axe z partant du sol et montant vers le ciel, alors
votre
force est positive car elle est dirigée sur cet axe, et le poids
est négatif, la somme des deux est donc nulle.
Un objet d'un certain poids fléchit une étagère,
plus l'étagère plie, plus elle oppose de force en sens
contraire de la cause qui la fait plier.
La planche fléchit jusqu'à ce que la force qu'elle exerce
équilibre le poids, ensuite il n'y a plus de mouvement, l'objet
reste immobile sur la planche.
Forces en équilibre dynamique.
Quand des forces ne sont pas en équilibre statique, elles sont
en équilibre dynamique, mais elles sont en équilibre
quand même.
Vous exercez une force F sur un objet en le poussant des deux mains,
mais vous ressentez une pression sur vos main et non une traction, ce
qui prouve que l'objet vous pousse comme vous, vous le poussez.
Vous communiquez une accélération a à l'objet
telle que F = ma
L'objet vous pousse avec la même force Fr = F, en toute logique
on devrait atteindre l'immobilité, mais ce n'est pas le cas car
la force Fr n'existe que parce qu'il y a accélération.
Un objet de masse m, qui tombe est soumis à la pesanteur due
à la terre, c'est à dire à son poids F=mg, et bien
sachez que si la terre exerce F=mg à l'objet, celui-ci lui
oppose une réaction Fr = ma telle que Fr = mg, c'est à
dire a = g, l'accélération de l'objet vaut g.
Prenons un exemple (on prendra g = 10).
Vous exercez une force de 30 N vers le haut, sur un objet de masse 2
kg, que se passe t-il?
La force exercée vers le haut est Fh = 30 N, c'est votre force.
Vers le bas, il y a le poids 20 N et la réaction de l'objet que
vous accélérez d'une valeur a, Soit FB = 20 + 2a
Les deux forces étant identiques, on obtient :
Fh = Fb + 30 = 20 + 2a, soit a = 5 m/s²
Le résultat de ces deux forces va accélérer
l'objet de 2 kg de 5m/s² vers le haut.
Autre exemple :
Soient trois forces tirant un objet dans des directions
différentes.
F1 = (10 N, 30°)
F2 = (20 N, 100°)
F3 = (15 N, 180°)
L'équilibre des trois forces est-il statique, sinon
décrire le mouvement de l'objet sachant que sa masse est de 500
g.
Vous pouvez additionner les vecteurs par construction à partir
d'un double décimètre et d'un rapporteur, ou encore
passer par la relation du triangle quelconque qui est assez lourde.
Le plus simple est de construire un système d'axes Oxy, tels que
les angles des vecteurs soient donnés par rapport à l'axe
Ox, par cette méthode il suffit de faire des sommes
algébriques.
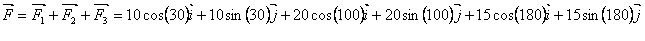
= (10cos30 + 20cos100 +
15cos180)i + (10sin30 +
20sin100 + 15sin180)j
F = -9,8i + 24,7j
Cette force n'est pas nulle, l'équilibre n'est pas statique.
Nous pouvons déterminer le module et la direction de cette force.
Module :
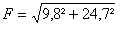
F = 26,6 N
Direction.
la composante négative sur l'axe Ox montre que la direction fait
un angle supérieur à 90°
On peut trouver le complément à 180°
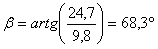
D'où la direction de la force :
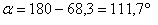
Puisque la force résultante est dirigée suivant un angle
qui fait 111,7° avec l'axe Ox, l'objet va se déplacer en
accélérant dans cette direction.
Le module de cette accélération est donné par :
F = ma = 26,6 N
a = F/m = 26,6/0,5 = 53,2 m.s-2
L'objet s'oppose à cette accélération sous la
forme d'une force résistante qui a la même valeur: 26,6 N,
mais le mouvement persiste je l'ai déjà dit, je sais.
Cette accélération est importante, elle vaut plus de 5
fois celle de la pesanteur, c'est parce que l'objet n'est pas massif,
500 g ce n'est pas grand chose, et si vous avez une masse plus faible,
l'accélération sera plus grande mais il y aura des
limites.
Vous ne pourrez pas augmenter indéfiniment
l'accélération en diminuant la masse de l'objet, votre
bras ne peut atteindre des vitesses fantastiques, si
l'accélération est grande, cela ne durera pas car la
vitesse va atteindre sa valeur limite.
Imaginez un système avec des engrenages pour multiplier la
vitesse de votre bras, vous allez rencontrer un autre problème,
c'est que si la masse de l'objet est petite, celle du mécanisme
formé par les rouages et les bras de levier sera assez
importante pour limiter les effets, et ne sera plus négligeable.
Ainsi, il n'est pas simple de communiquer une force importante à
un objet petit.
Par exemple si vous soulevez un sac de ciment de 40 kg, vous exercez
une force de 400 N (g environ 10), imaginez que vous arriviez
à communiquer la même force à une puce, quelle va
être l'accélération de votre main ? et en admettant
que vous y parveniez quelle va être la force communiquée
à votre main et quelle va être la force communiquée
à votre bras?
Je ne connais pas la masse d'une puce et je n'ai pas envie de chercher,
cet exemple sert à vous démontrer que pour traiter un
problème de physique, il faut se placer dans un monde ou les
éléments sont à la même échelle, et
si on ne le fait pas, il faut reformer le modèle car celui de
base n'est pas suffisant.
Les problèmes de physique font toujours appel à des
formules et à un modèle qu'il ne faut pas prendre trop
simple, les résultats seraient faux, ni trop compliqués,
car la précision serait inutile si on donnait 10 chiffres
après la virgule.
Exemple :
Vous accélérez un objet de masse 1 kg en exerçant
une
force de 10 N, quelle est la valeur de l'accélération.
Premier modèle :
Une sphère en métal immobile dans le vide le plus
poussé.
Non seulement les molécules de gaz sont rares mais la prise au
vent d'une sphère est négligeable aux faibles vitesses.
La simple relation F = ma suffit.
Deuxième modèle :
Le même que le premier mais on est dans l'air.
On peut encore utiliser F = ma, mais pas longtemps, dès que la
vitesse va devenir importante, la résistance de l'air due aux
frottements va se faire sentir.
Troisième modèle :
Cette fois, on remplace la sphère par une tôle.
Ce modèle peut se décomposer en sous modèles,
est-ce que la tôle tombe à plat ou sur la tranche,
Vous comprenez maintenant que l'on ne peut pas toujours utiliser
brutalement F=ma, ce n'est pas la formule qui n'est pas bonne, c'est le
modèle.
Bien évidemment, les professeurs, dans leurs exercices utilisent
les bons modèles, ils ne vont pas vous donner un problème
dans lequel vous ferez intervenir la résistance de l'air si
aucune donnée telle le coefficient de frottement, de forme etc
n'apparaît dans l'énoncé.
Il arrive même que l'énoncé précise ce qui
doit être négligé.
En gros, vous n'aurez pas trop de soucis de modélisation dans un
problème d'examen, mais vous en aurez dans les problèmes
que vous allez vous poser.
Nous venons de terminer l'équilibre des forces.
Pas de mouvement, la somme des forces est nulle, l'équilibre est
statique.
Mouvement uniformément accéléré, la somme
des forces est toujours nulle, l'équilibre est dynamique.
Remarque :
Nous rencontrons souvent des figures où il n'y a pas
d'équilibre des forces mais c'est uniquement parce qu'elles ne
sont pas toutes représentées, dans un système, on
ne parle pas obligatoirement des forces résistantes, c'est par
pur soucis de simplification, mais ces forces existent.
Exemple, on tire une masse de 5 kg avec un effort de 50 N, celle-ci
s'accélère de 10 m/s/s on applique F = ma, il n'y a
qu'une force, ce n'est pas que la réaction n'existe pas, c'est
qu'elle n'est pas utile pour calculer l'accélération.
Pourquoi écrire FT+FR = 0 avec FT (traction) FR
(réaction) puis FT = maT FR = -maR
Ecrire F = ma suffit largement.
Souvent, on ne compte que les forces motrices (celles qui engendrent
des déplacement ou qui les modifie), il faut bien en être
conscient, il y a toujours équilibre.
Par contre une chose est importante :
TOUTES LES FORCES DOIVENT AVOIR LE MEME POINT D'APPLICATION
Nous verrons plus loin comment s'équilibrent des forces dont les
points d'applications sont différents, nous montrerons
d'ailleurs qu'elles ne s'équilibrent pas, que c'est leur moment
qui s'équilibre.
On n'additionne pas des forces qui n'ont pas un point d'application
commun, il ne s'agit pas de faire glisser un vecteur à
l'extrémité d'un autre, une force n'est pas un vecteur
mais un représentant d'une classe de vecteurs.
Je ne tiens pas à alourdir ce document par une grande
série de problèmes, vous trouverez pas mal d'exercices
sur des livres de cours ou des annales d'examen, il n'y a pas de
secret, il faut en faire plein si on veut devenir fort.
Il serait naturel de penser qu'une force s'exerce par contact entre la
source motrice et l'objet que l'on met en mouvement et que ce contact
est indispensable.
Pourtant nul n'ignore qu'un aimant est capable d'attirer le fer
à distance, et que la planète terre attire tous les
objets, il en est de même d'ailleurs des autres planètes,
un objet placé en l'air sur
mars va aussi tomber au sol.
Ces deux cas font l'objet de forces de nature différente, nous
allons citer les 5 types de forces connues ce jour.
La première :
Loi de gravitation universelle.
Cette loi a été énoncée par Newton, elle
concerne tous les objets.
Deux objets de masse m1 et m2 placés seuls dans l'espace
s'attirent avec une force qui vaut :
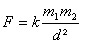
k : constante = 6,62x10^-11
d : distance entre les objets.
Si les objets ne sont pas seuls dans l'espace, la force d'attraction
des deux objets s'ajoutent à celle due aux autres objets.
Portée de l'interaction : elle est infinie, mais comme la
relation l'indique, elle diminue rapidement avec la distance.
Puisque cette loi concerne tous les objets, on comprend maintenant
qu'un homme puisse tomber sur la lune car la lune et l'homme s'attirent
conformément à la relation.
La terre attirait les trois astronautes avant qu'ils ne partent sur la
lune, elle continuait à les attirer quand ils sont
arrivés mais faiblement car ils étaient loin.
La lune attirait faiblement les astronautes quand ils étaient
sur terre, mais en raison de la distance la force était faible,
celle-ci était plus forte quand ils sont arrivés.
Les trois astronautes s'attiraient entre eux à tout moment, mais
la force d'attraction est imperceptible car les masses mises en jeu
sont très faible, il faut que l'une d'elle soit de l'ordre de
celle d'un astre pour que l'effet soit important.
Donc pour résumer :
Tous les objets s'attirent, pour que la force soit appréciable,
il faut :
Que la distance qui sépare les objets soit le plus faible
possible, c'est à dire de l'ordre du rayon du plus gros objet.
Que l'un des objet soit un astre.
Pourtant:
L'effet est quand même visible si ces conditions ne sont pas tout
à fait respectées.
Le soleil et la lune qui sont loin, attirent l'eau des mers et des
océans, c'est ce phénomène qui provoque les
marées.
L'attraction de deux objets massifs a pu être mesurée
à l'aide d'une balance à torsion, c'est cette mesure qui
a permis de fournir la valeur de k.
Mais la mesure est délicate, car elle est faite sur terre, et la
terre attire davantage les objets qu'ils ne s'attirent entre eux.
Cette mesure de k permet de connaître la masse de toutes les
planètes.
Gravitation des planètes et des satellites
La terre et la lune s'attirent, mais alors pourquoi la lune ne tombe
t-elle pas sur la terre?
La lune tourne autour de la terre, il existe donc une force centrifuge
qui a tendance à éloigner la lune de la terre, cette
force est compensée par l'attraction entre ces deux astres, la
distance reste donc constante;
Masse de la planète terre.
Une masse m est attirée par la terre de masse M avec une force
de :
F = kMm/R²
R est le rayon de la terre, c'est aussi la distance entre le centre de
la terre et celui de l'objet.
On sait que la force d'attraction de l'objet par la terre n'est
autre que son poids donné par :
F = mg
g = 9,81 m/s²
En égalisant ces deux relations :
kMm/R² = mg
kM/R² = g
M = gR²/k
M = 9,81x6366000²/6,67E-11
M = 5,96x10^24 kg
Exercice d'application :
A quelle altitude sont placés les satellites
géostationnaires de télécommunication, pourquoi
ceux-ci sont ils au dessus de l'équateur.
Par définition, un satellite est dit géostationnaire,
s'il est visible du sol 24h/24h c'est à dire qu'il est
entraîné à la même vitesse angulaire que la
terre.
La réponse est donnée un peu plus loin.
La deuxième :
La force électrostatique connue
sous le nom de loi de Coulomb.
C'est la deuxième force que l'on connait avec la force
magnétique, on n'en fait qu'une que l'on désigne sous le
nom de force électromagnétique.
Contrairement à la loi d'attraction universelle, la force de
Coulomb ne s'exerce que sur des particules électriques, mais
l'intensité est beaucoup plus importante.
La formule de Coulomb ressemble beaucoup à celle de Newton.
F = kQ1Q2/r²
Q1 et Q2 sont deux charges électriques, et R la distance
entre les deux.
k = 0,885x10^-11
Il existe deux types de charges, les charges positives et les charges
négatives, ce qui fait que suivant leur signe respectif, les
charges peuvent s'attirer ou se repousser.
Deux charges de même signe se repoussent et deux charges de
même signe s'attirent.
Si on trace un système d'axe Ox, et que l'on place une charge Q1
en O et une charge Q2 quelque part sur l'axe x, la force sera positive
si elle est dirigée dans le sens des x positifs et
négative dans le sens contraire, soit :
F = k(Q1Q2x/abs(x)^3)i
Réponse à l'exercice
précédent.
Le satellite est géostationnaire, sa vitesse angulaire est donc
de 360°/24 h
Soit w = 2p/(24x60x3600) rd/s
La force centrifuge exercée par un satellite de masse m, vaut :
F = mw²(R+H), avec :
R = rayon de la terre et H altitude.
La troisième :
La force
électromagnétique aboutissant à la
définition de l'Ampère.
Voici comment on définit l'ampère.
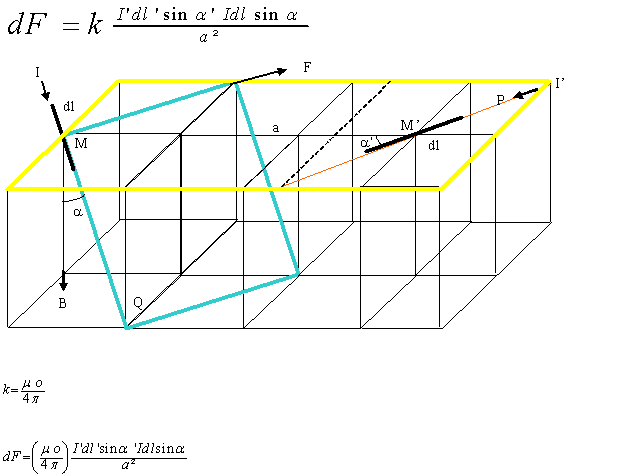
Deux fils parallèles de section uniforme et négligeable,
espacés de 1 mètre et parcourus par un courant de 1
Ampère exerce une force de 2x10^-7 N par mètre de
longueur.
Les fils s'attirent si les courants circulent dans le même sens,
sinon ils se repoussent.
Expérimentalement, il a été montré que la
force était proportionnelle à la longueur des fils, au
courant qui circulent dans chacun d'eux et inversement proportionnelle
au carré de la distance qui les sépare, ce qui fait pour
deux brins dl et dl' traversés par des courants I et I', et
séparés d'une distance r.
dF = kdl.dl'.I.I'/r²
Cette relation exige que les fils soient parallèles, et que les
brins soient face à face, c'est à dire que le vecteur r
est orthogonal aux brins.
Si les brins font un angle a et a' par rapport au rayon alors la loi se
généralise.
dF = kdl.dl'.I.I'sina.sina'/r²
Avec k = µo/4pi
La direction de la force devient plus compliquée quand les fils
sont alignés, d'ailleurs la force exercée par le premier
conducteur sur le deuxième n'est pas dirigée comme celle
de la force exercée par le deuxième conducteur sur le
premier.
Il n'est pas utile de s'attarder sur ce point, ce chapitre n'a pour but
que de présenter les différentes forces, chacune d'elle
doit faire appel à des cours spéciaux.
N'importe quel traité d'électromagnétisme
présente ce type de force.
Un dessin en 3D est toujours compliqué à
interpréter car on n'a que le plan pour le représenter.
Il existe une formule qui utilise le produit vectoriel, la voici:
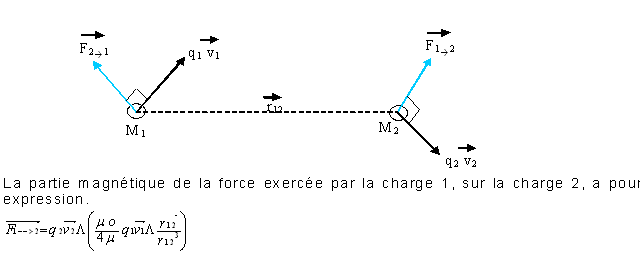
Nous n'insisterons pas sur cette force, elle fait l'objet d'un cours
d'électromagnétisme que l'on ne peut détailler en
quelques lignes.
La quatrième :
Forces d'interaction faible
ce type de force se rencontre dans les noyaux atomiques.
Ce type de force est décrit sur le site ci-dessous:
http://www.cerimes.education.fr/e_doc/forces/faible.htm
La cinquième
Force d'interaction forte.
Aucune force au monde ne pourrait faire lâcher la noisette tenue
par
l'écureuil de l'age de glace.
De même on ne connait aucune force supérieure à
celle qui maintient les protons dans le noyau atomique.
Le noyau atomique est constitué de protons qui se repoussent
parce qu'ils sont de même signe, et pourtant le noyau garde sa
cohésion;
Le fait est qu'il existe une force bien supérieure à
celle
de coulomb, appelée "interaction forte" mais dont la
portée est très réduite.
Un noyau qui comprend plus de neutrons que de protons devient instable,
car ceux-ci ne peuvent rester côte à côte,
l'interaction forte perd de son intensité.
UNIFICATION
Les physiciens recherchent à unifier toutes les forces pour n'en
faire qu'une, on sait aujourd'hui que la force magnétique et la
force électrique sont en étroite relation, pour former ce
que l'on nomme force électromagnétique.
EN RESUME
Ces forces ne sont pas approfondies ici, car il faudrait un ouvrage
complet pour chaque type de force.
La force d'attraction universelle fait l'objet de la mécanique
classique et de la relativité générale pour ceux
qui veulent approfondir le sujet;
La force de Coulomb est étudiée en détail sur les
traités d'électrostatique, des livres
d'électromagnétismes vous révèleront la
nature des forces magnétiques.
Les forces d'interaction faibles et fortes sont traitées dans
des ouvrages de physique nucléaire et certains livre de physique
quantique.
CONCLUSION
Les forces ont été présentées de
façon sommaire pour pouvoir aborder les différents sujets
de la physique comme la mécanique et
l'électromagnétisme.
Chaque partie couvre un, voire plusieurs livre, par exemple la
mécanique requière un volume pour la mécanique
classique, un pour la mécanique relativiste et un pour la
mécanique quantique.
Je souhaite que cet exposé a attiré votre attention, tout
ne pouvait figurer ici.