Ce mot "coniques" a un sens, il vient du mot cône, et s'il est au
pluriel c'est parce qu'il y en a plusieurs, plus exactement trois si on
ne compte pas les cas particuliers.
Mais il y a plusieurs définitions possibles.
La première issue du cône et qui aboutit à
l'équation réduite par translation du repère,
amenant l'origine des axes Ox et Oy au centre..
La deuxième utilise une forme générale applicable
à toutes les coniques.
Enfin la troisième est définie par rapport à
l'excentricité, les foyers et les directrices.
Voyons ces trois définitions, mieux vaut adopter la
première comme originale puisqu'elle provient du cône, et
vérifier que l'on peut passer aux deux autres définitions
par certaines opérations qui sont :
Le décalage de repère.
L'agrandissement ou la réduction du graphique.
La rotation du repère.
Voyons en détail ces trois définitions.
Cette page ne fait que présenter les principales relations, pour
les démonstrations, cliquer sur les liens.
I. Définition à partir du
cône
C'est à partir de cette définition que je suis
arrivé aux formes réduites, ce qui n'empêche pas
d'y parvenir à partir des deux autres.
Observons les trois cas ci-dessous.
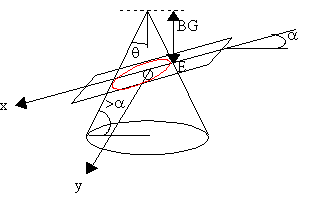

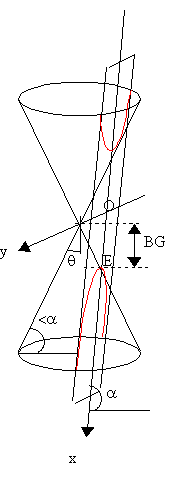
Le dessin de gauche montre une ellipse, seul cas où
la courbe se referme, cela se produit lorsque le plan de coupe est
moins incliné que les génératrices du cône.
L'équation est donnée par :
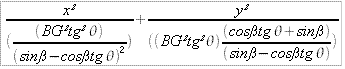
Ce qui correspond à la
forme réduite :
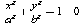
Le dessin du milieu est une parabole,
il correspond au cas où le plan de coupe a même
inclinaison que les génératrices du cône.
L'équation est donnée par :
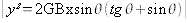
Ce qui correspond à la
forme réduite :
y² = 2px
Le dessin de droite est une hyperbole, il correspond au cas où
le plan de coupe est plus incliné que les
génératrices du cône, un des cas particulier est
celui où le plan de coupe est vertical, ce cas est aussi une hyperbole.
L'équation est donnée par :
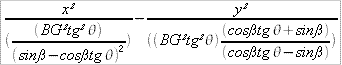
Ce qui correspond à la
forme réduite :
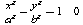
Il n'est pas utile de retenir ces formules par coeur, il suffit de les
noter et de les utiliser chaque fois que l'on voudra déterminer
l'équation de la courbe engendrée par un cône,
comme par exemple l'ombre d'un lampadaire sur un mur.
par contre les formes réduites sont à connaître si
les coniques sont au programme d'un examen, elles ne sont pas
très compliquées par leur forme;
La démonstration de ces formules est traitée dans le
document ci-dessous :
coniques_edition
2
II. Equation générale
d'une conique.
L'équation générale a pour avantage de
décrire une conique situé à un emplacement
quelconque du plan, et d'être unique dans sa forme qui est :
ax²+bxy+cy²+dx+ey+f=0
Certains auteurs mettent un coefficient 2 en facteur avec x et y, cela
ne change rien.
Une règle est essentielle pour une conique, les trois
coefficients a b et c ne doivent pas être tous nuls.
Mais alors, si cette équation est unique, comment savoir si on a
affaire à une ellipse, à une parabole ou à une
hyperbole?
Cette réponse est donnée en observant le signe de
b²-ac, il y a une démonstration dans le document joint, le
Larousse illustré fournit une démonstration
différente en parlant des asymptotes.
La parabole a pour asymptote la tangente au sommet elle correspond au
cas b²-ac = 0
L'ellipse n'a pas de points x et y infinis, donc pas d'asymptotes, elle
correspond au cas b²-ac<0
l'hyperbole a pour asymptote, deux droites sécantes, elle
correspond au cas b²-ac>0
Voir définition du Larousse
III. Définition à partir
de l'excentricité et des foyers
Si vous avez épluché à fond les deux
premières définitions, c'est encore insuffisant pour
traiter de problèmes sur les coniques, il vaut mieux survoler
les trois définitions que connaître entièrement les
deux premières.
En effet, tous les ouvrages sur l'astronomie parlent de foyer et
d'excentricité pour décrire le mouvement des corps
célestes telles les planètes.
Une planète dont l'excentricité de l'orbite est voisin de
0, signifie que la révolution est presque un cercle, au
contraire si l'excentricité approche 1, la forme est une ellipse
très "aplatie".
Si l'excentricité d'une comète est égale à
1, la trajectoire est une parabole, la comète ne reviendra plus
au voisinage de la terre.
Traitons maintenant cette troisième définition.
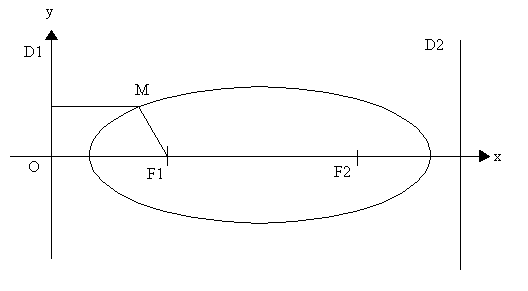
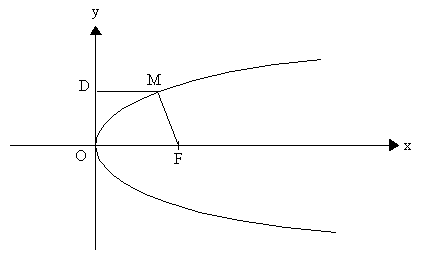
Une conique est formée par l'ensemble des points tels que le
rapport entre MF et MD est égal à une constante e qui est
l'excentricité.
Le point F est nommé foyer et se trouve sur l'axe Ox
MD est la distance entre chaque point M de la courbe et une droite D
qui n'est autre que l'axe Oy et que l'on nomme directrice.
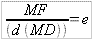
Pour l'ellipse et pour l'hyperbole, il y a deux foyers F1 et F2 et deux
directrices D1 et D2, on peut faire référence à F1
et D1 ou F2 et D2, ainsi avons nous pour tout point M.
MF1/d(MD1) = e et MF2/d(MD2) = e
Ellipse cas où e < 1
Parabole cas où e = 1
Hyperbole cas où e>1

Pour plus de détail voir le document ci-dessous
voir coniques
foyers
Ce document traite aussi d'une définition par rapport aux deux
foyers, et indique comment tracer la courbe à l'aide d'une
ficelle (voire deux) et un crayon.
IV. Equation en coordonnées
polaires
L'écriture en coordonnées polaires peut être
intéressante pour des applications de mécanique
céleste.
voir coniques compléments
CONCLUSION
Cette étude semble assez compliquée mais elle est aussi
assez complète, il n'est pas obligatoire de tout étudier
pour traiter les problèmes sur les coniques.
On retiendra juste les formes réduites, l'équation
générale et la définition par foyer et directrice,
car il est rare que l'on cherche à passer d'une forme à
une autre, d'habitude, on part d'une forme qui semble la mieux
appropriée pour traiter d'un problème et on s'y tient.
Avant de quitter ce site, vous pouvez aller faire un tour sur
wikipedia, ce que vous allez y trouver n'est pas de moi, mais c'est
très intéressant.
http://www.sciences.univ-nantes.fr/physique/perso/gtulloue/Coniques/Index_coniques.html